走近源码：神奇的HyperLogLog

HyperLogLog是Redis的高级数据结构，是统计基数的利器。前文我们已经介绍过HyperLogLog的基本用法，如果只求会用，只需要掌握HyperLogLog的三个命令即可，如果想要更进一步了解HyperLogLog的原理以及源码实现，相信这篇文章会给你带来一些启发。

基数

在数学上，基数或势，即集合中包含的元素的“个数”（参见势的比较），是日常交流中基数的概念在数学上的精确化（并使之不再受限于有限情形）。有限集合的基数，其意义与日常用语中的“基数”相同，例如{\displaystyle {a,b,c}}的基数是3。无限集合的基数，其意义在于比较两个集的大小，例如整数集和有理数集的基数相同；整数集的基数比实数集的小。

在介绍HyperLogLog的原理之前，请你先来思考一下，如果让你来统计基数，你会用什么方法。

Set

熟悉Redis数据结构的同学一定首先会想到Set这个结构，我们只需要把数据都存入Set，然后用scard命令就可以得到结果，这是一种思路，但是存在一定的问题。如果数据量非常大，那么将会耗费很大的内存空间，如果这些数据仅仅是用来统计基数，那么无疑是造成了巨大的浪费，因此，我们需要找到一种占用内存较小的方法。

bitmap

bitmap同样是一种可以统计基数的方法，可以理解为用bit数组存储元素，例如01101001，表示的是[1,2,4,8]，bitmap中1的个数就是基数。bitmap也可以轻松合并多个集合，只需要将多个数组进行异或操作就可以了。bitmap相比于Set也大大节省了内存，我们来粗略计算一下，统计1亿个数据的基数，需要的内存是：100000000/8/1024/1024 ≈ 12M。

虽然bitmap在节省空间方面已经有了不错的表现，但是如果需要统计1000个对象，就需要大约12G的内存，显然这个结果仍然不能令我们满意。在这种情况下，HyperLogLog将会出来拯救我们。

HyperLogLog原理

HyperLogLog实际上不会存储每个元素的值，它使用的是概率算法，通过存储元素的hash值的第一个1的位置，来计算元素数量。这么说不太容易理解，容我先搬出来一个栗子。

有一天Jack和丫丫玩抛硬币的游戏，规则是丫丫负责抛硬币，每次抛到正面为一回合，丫丫可以自己决定进行几个回合。最后需要告诉Jack最长的那个回合抛了多少次，再由Jack来猜丫丫一共进行了几个回合。Jack心想：这可不好猜啊，我得算算概率了。于是在脑海中绘制这样一张图。

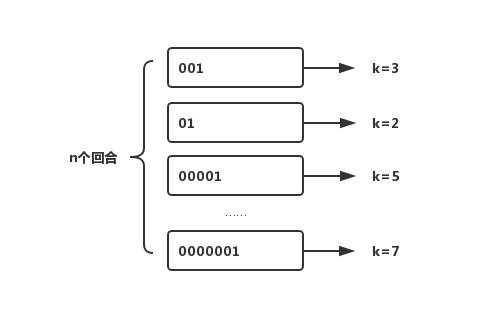
k是每回合抛到1所用的次数，我们已知的是最大的k值，可以用k_max表示，由于每次抛硬币的结果只有0和1两种情况，因此，k_max在任意回合出现的概率即为(1/2)^k_max，因此可以推测n=2^k_max。概率学把这种问题叫做伯努利实验。此时丫丫已经完成了n个回合，并且告诉Jack最长的一次抛了3次，Jack此时也胸有成竹，马上说出他的答案8，最后的结果是：丫丫只抛了一回合，Jack输了，要负责刷碗一个月。

终于，我们的Philippe Flajolet教授遇到了Jack一样的问题，他决心吸取Jack的教训，要让这个算法更加准确，于是引入了桶的概念，计算m个桶的加权平均值，这样就能得到比较准确的答案了（实际上还要进行其他修正）。最终的公式如图

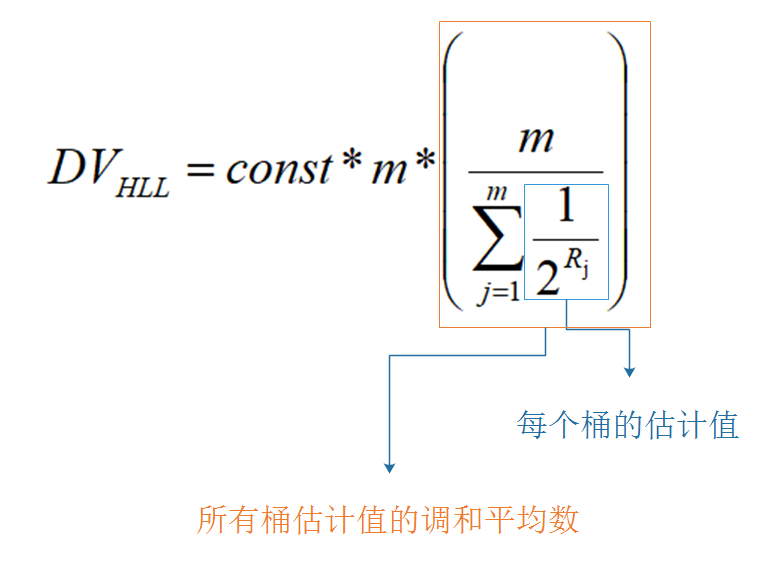
其中m是桶的数量，const是修正常数，它的取值会根据m而变化。p=log₂m

switch (p) {
   case 4:
       constant = 0.673 * m * m;
   case 5:
       constant = 0.697 * m * m;
   case 6:
       constant = 0.709 * m * m;
   default:
       constant = (0.7213 / (1 + 1.079 / m)) * m * m;
}

我们回到Redis，对于一个输入的字符串，首先得到64位的hash值，用前14位来定位桶的位置（共有2¹⁴，即16384个桶）。后面50位即为伯努利过程，每个桶有6bit，记录第一次出现1的位置count，如果count>oldcount，就用count替换oldcount。

了解原理之后，我们再来聊一下HyperLogLog的存储。HyperLogLog的存储结构分为密集存储结构和稀疏存储结构两种，默认为稀疏存储结构，而我们常说的占用12K内存的则是密集存储结构。

密集存储结构

密集存储比较简单，就是连续16384个6bit的串成的位图。由于每个桶是6bit，因此对桶的定位要麻烦一些。

#define HLL_BITS 6 /* Enough to count up to 63 leading zeroes. */
#define HLL_REGISTER_MAX ((1<<HLL_BITS)-1)
/* Store the value of the register at position 'regnum' into variable 'target'.
 * 'p' is an array of unsigned bytes. */
#define HLL_DENSE_GET_REGISTER(target,p,regnum) do { \
    uint8_t *_p = (uint8_t*) p; \
    unsigned long _byte = regnum*HLL_BITS/8; \
    unsigned long _fb = regnum*HLL_BITS&7; \
    unsigned long _fb8 = 8 - _fb; \
    unsigned long b0 = _p[_byte]; \
    unsigned long b1 = _p[_byte+1]; \
    target = ((b0 >> _fb) | (b1 << _fb8)) & HLL_REGISTER_MAX; \
} while(0)

/* Set the value of the register at position 'regnum' to 'val'.
 * 'p' is an array of unsigned bytes. */
#define HLL_DENSE_SET_REGISTER(p,regnum,val) do { \
    uint8_t *_p = (uint8_t*) p; \
    unsigned long _byte = regnum*HLL_BITS/8; \
    unsigned long _fb = regnum*HLL_BITS&7; \
    unsigned long _fb8 = 8 - _fb; \
    unsigned long _v = val; \
    _p[_byte] &= ~(HLL_REGISTER_MAX << _fb); \
    _p[_byte] |= _v << _fb; \
    _p[_byte+1] &= ~(HLL_REGISTER_MAX >> _fb8); \
    _p[_byte+1] |= _v >> _fb8; \
} while(0)

如果我们要定位的桶编号为regnum，它的偏移字节量为(regnum 6) / 8，起始bit偏移为(regnum 6) % 8，例如，我们要定位编号为5的桶，字节偏移是3，位偏移也是6，也就是说，从第4个字节的第7位开始是编号为3的桶。这里需要注意，字节序和我们平时的字节序相反，因此需要进行倒置。我们用一张图来说明Redis是如何定位桶并且得到存储的值（即HLL_DENSE_GET_REGISTER函数的解释）。

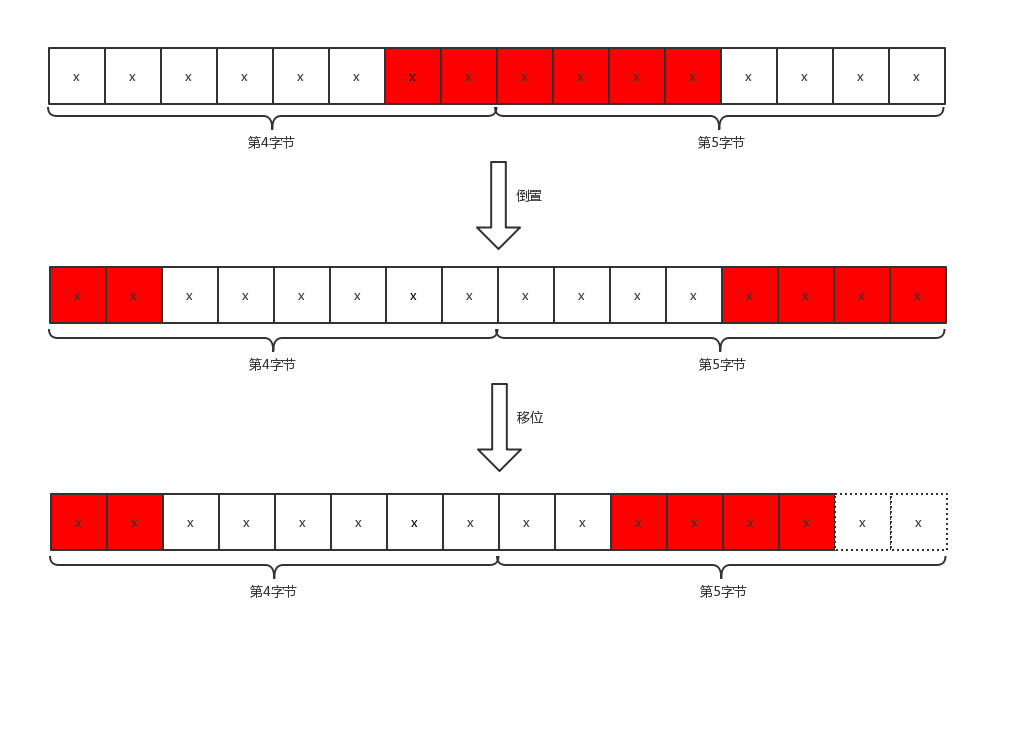
对于编号为5的桶，我们已经得到了字节偏移_byte和为偏移_fb，b0 >> _fb和b1 << _fb8操作是将字节倒置，然后进行拼接，并且保留最后6位。

稀疏存储结构

你以为Redis真的会用16384个6bit存储每一个HLL对象吗，那就too naive了，虽然它只占用了12K内存，但是Redis对于内存的节约已经到了丧心病狂的地步了。因此，如果比较多的计数值都是0，那么就会采用稀疏存储的结构。

对于连续多个计数值为0的桶，Redis使用的存储方式是：00xxxxxx，前缀两个0，后面6位的值加1表示有连续多少个桶的计数值为0，由于6bit最大能表示64个桶，所以Redis又设计了另一种表示方法：01xxxxxx yyyyyyyy，这样后面14bit就可以表示16384个桶了，而一个初始状态的HyperLogLog对象只需要用2个字节来存储。

如果连续的桶数都不是0，那么Redis的表示方式为1vvvvvxx，即为连续(xx+1)个桶的计数值都是(vvvvv+1)。例如，10011110表示连续3个8。这里使用5bit，最大只能表示32。因此，当某个计数值大于32时，Redis会将这个HyperLogLog对象调整为密集存储。

Redis用三条指令来表达稀疏存储的方式：

1. ZERO:len 单个字节表示 00[len-1]，连续最多64个零计数值
2. VAL:value,len 单个字节表示 1[value-1][len-1]，连续 len 个值为 value 的计数值
3. XZERO:len 双字节表示 01[len-1]，连续最多16384个零计数值

Redis从稀疏存储转换到密集存储的条件是：

1. 任意一个计数值从 32 变成 33，因为VAL指令已经无法容纳，它能表示的计数值最大为 32
2. 稀疏存储占用的总字节数超过 3000 字节，这个阈值可以通过 hll_sparse_max_bytes 参数进行调整。

源码解析

接下来通过源码来看一下pfadd和pfcount两个命令的具体流程。在这之前我们首先要了解的是HyperLogLog的头结构体和创建一个HyperLogLog对象的步骤。

HyperLogLog头结构体

struct hllhdr {
    char magic[4];      /* "HYLL" */
    uint8_t encoding;   /* HLL_DENSE or HLL_SPARSE. */
    uint8_t notused[3]; /* Reserved for future use, must be zero. */
    uint8_t card[8];    /* Cached cardinality, little endian. */
    uint8_t registers[]; /* Data bytes. */
};

创建HyperLogLog对象

#define HLL_P 14 /* The greater is P, the smaller the error. */
#define HLL_REGISTERS (1<<HLL_P) /* With P=14, 16384 registers. */
#define HLL_SPARSE_XZERO_MAX_LEN 16384


#define HLL_SPARSE_XZERO_SET(p,len) do { \
    int _l = (len)-1; \
    *(p) = (_l>>8) | HLL_SPARSE_XZERO_BIT; \
    *((p)+1) = (_l&0xff); \
} while(0)

/* Create an HLL object. We always create the HLL using sparse encoding.
 * This will be upgraded to the dense representation as needed. */
robj *createHLLObject(void) {
    robj *o;
    struct hllhdr *hdr;
    sds s;
    uint8_t *p;
    int sparselen = HLL_HDR_SIZE +
                    (((HLL_REGISTERS+(HLL_SPARSE_XZERO_MAX_LEN-1)) /
                     HLL_SPARSE_XZERO_MAX_LEN)*2);
    int aux;

    /* Populate the sparse representation with as many XZERO opcodes as
     * needed to represent all the registers. */
    aux = HLL_REGISTERS;
    s = sdsnewlen(NULL,sparselen);
    p = (uint8_t*)s + HLL_HDR_SIZE;
    while(aux) {
        int xzero = HLL_SPARSE_XZERO_MAX_LEN;
        if (xzero > aux) xzero = aux;
        HLL_SPARSE_XZERO_SET(p,xzero);
        p += 2;
        aux -= xzero;
    }
    serverAssert((p-(uint8_t*)s) == sparselen);

    /* Create the actual object. */
    o = createObject(OBJ_STRING,s);
    hdr = o->ptr;
    memcpy(hdr->magic,"HYLL",4);
    hdr->encoding = HLL_SPARSE;
    return o;
}

这里sparselen=HLL_HDR_SIZE+2，因为初始化时默认所有桶的计数值都是0。其他过程不难理解，用的存储方式是我们前面提到过的稀疏存储，创建的对象实质上是一个字符串对象，这也是字符串命令可以操作HyperLogLog对象的原因。

PFADD命令

/* PFADD var ele ele ele ... ele => :0 or :1 */
void pfaddCommand(client *c) {
    robj *o = lookupKeyWrite(c->db,c->argv[1]);
    struct hllhdr *hdr;
    int updated = 0, j;

    if (o == NULL) {
        /* Create the key with a string value of the exact length to
         * hold our HLL data structure. sdsnewlen() when NULL is passed
         * is guaranteed to return bytes initialized to zero. */
        o = createHLLObject();
        dbAdd(c->db,c->argv[1],o);
        updated++;
    } else {
        if (isHLLObjectOrReply(c,o) != C_OK) return;
        o = dbUnshareStringValue(c->db,c->argv[1],o);
    }
    /* Perform the low level ADD operation for every element. */
    for (j = 2; j < c->argc; j++) {
        int retval = hllAdd(o, (unsigned char*)c->argv[j]->ptr,
                               sdslen(c->argv[j]->ptr));
        switch(retval) {
        case 1:
            updated++;
            break;
        case -1:
            addReplySds(c,sdsnew(invalid_hll_err));
            return;
        }
    }
    hdr = o->ptr;
    if (updated) {
        signalModifiedKey(c->db,c->argv[1]);
        notifyKeyspaceEvent(NOTIFY_STRING,"pfadd",c->argv[1],c->db->id);
        server.dirty++;
        HLL_INVALIDATE_CACHE(hdr);
    }
    addReply(c, updated ? shared.cone : shared.czero);
}

PFADD命令会先判断key是否存在，如果不存在，则创建一个新的HyperLogLog对象；如果存在，会调用isHLLObjectOrReply()函数检查这个对象是不是HyperLogLog对象，检查方法主要是检查魔数是否正确，存储结构是否正确以及头结构体的长度是否正确等。

一切就绪后，才可以调用hllAdd()函数添加元素。hllAdd函数很简单，只是根据存储结构判断需要调用hllDenseAdd()函数还是hllSparseAdd()函数。

密集存储结构只是比较新旧计数值，如果新计数值大于就计数值，就将其替代。

而稀疏存储结构要复杂一些：

1. 判断是否需要调整为密集存储结构，如果不需要则继续进行，否则就先调整为密集存储结构，然后执行添加操作
2. 我们需要先定位要修改的字节段，通过循环计算每一段表示的桶的范围是否包括要修改的桶
3. 定位到桶后，如果这个桶已经是VAL，并且计数值大于当前要添加的计数值，则返回0，如果小于当前计数值，就进行更新
4. 如果是ZERO，并且长度为1，那么可以直接把它替换为VAL，并且设置计数值
5. 如果不是上述两种情况，则需要对现有的存储进行拆分

PFCOUNT命令

/* PFCOUNT var -> approximated cardinality of set. */
void pfcountCommand(client *c) {
    robj *o;
    struct hllhdr *hdr;
    uint64_t card;

    /* Case 1: multi-key keys, cardinality of the union.
     *
     * When multiple keys are specified, PFCOUNT actually computes
     * the cardinality of the merge of the N HLLs specified. */
    if (c->argc > 2) {
        uint8_t max[HLL_HDR_SIZE+HLL_REGISTERS], *registers;
        int j;

        /* Compute an HLL with M[i] = MAX(M[i]_j). */
        memset(max,0,sizeof(max));
        hdr = (struct hllhdr*) max;
        hdr->encoding = HLL_RAW; /* Special internal-only encoding. */
        registers = max + HLL_HDR_SIZE;
        for (j = 1; j < c->argc; j++) {
            /* Check type and size. */
            robj *o = lookupKeyRead(c->db,c->argv[j]);
            if (o == NULL) continue; /* Assume empty HLL for non existing var.*/
            if (isHLLObjectOrReply(c,o) != C_OK) return;

            /* Merge with this HLL with our 'max' HHL by setting max[i]
             * to MAX(max[i],hll[i]). */
            if (hllMerge(registers,o) == C_ERR) {
                addReplySds(c,sdsnew(invalid_hll_err));
                return;
            }
        }

        /* Compute cardinality of the resulting set. */
        addReplyLongLong(c,hllCount(hdr,NULL));
        return;
    }

    /* Case 2: cardinality of the single HLL.
     *
     * The user specified a single key. Either return the cached value
     * or compute one and update the cache. */
    o = lookupKeyWrite(c->db,c->argv[1]);
    if (o == NULL) {
        /* No key? Cardinality is zero since no element was added, otherwise
         * we would have a key as HLLADD creates it as a side effect. */
        addReply(c,shared.czero);
    } else {
        if (isHLLObjectOrReply(c,o) != C_OK) return;
        o = dbUnshareStringValue(c->db,c->argv[1],o);

        /* Check if the cached cardinality is valid. */
        hdr = o->ptr;
        if (HLL_VALID_CACHE(hdr)) {
            /* Just return the cached value. */
            card = (uint64_t)hdr->card[0];
            card |= (uint64_t)hdr->card[1] << 8;
            card |= (uint64_t)hdr->card[2] << 16;
            card |= (uint64_t)hdr->card[3] << 24;
            card |= (uint64_t)hdr->card[4] << 32;
            card |= (uint64_t)hdr->card[5] << 40;
            card |= (uint64_t)hdr->card[6] << 48;
            card |= (uint64_t)hdr->card[7] << 56;
        } else {
            int invalid = 0;
            /* Recompute it and update the cached value. */
            card = hllCount(hdr,&invalid);
            if (invalid) {
                addReplySds(c,sdsnew(invalid_hll_err));
                return;
            }
            hdr->card[0] = card & 0xff;
            hdr->card[1] = (card >> 8) & 0xff;
            hdr->card[2] = (card >> 16) & 0xff;
            hdr->card[3] = (card >> 24) & 0xff;
            hdr->card[4] = (card >> 32) & 0xff;
            hdr->card[5] = (card >> 40) & 0xff;
            hdr->card[6] = (card >> 48) & 0xff;
            hdr->card[7] = (card >> 56) & 0xff;
            /* This is not considered a read-only command even if the
             * data structure is not modified, since the cached value
             * may be modified and given that the HLL is a Redis string
             * we need to propagate the change. */
            signalModifiedKey(c->db,c->argv[1]);
            server.dirty++;
        }
        addReplyLongLong(c,card);
    }
}

如果要计算多个HyperLogLog的基数，则需要将多个HyperLogLog对象合并，这里合并方法是将所有的HyperLogLog对象合并到一个名为max的对象中，max采用的是密集存储结构，如果被合并的对象也是密集存储结构，则循环比较每一个计数值，将大的那个存入max。如果被合并的是稀疏存储，则只需要比较VAL即可。

如果计算单个HyperLogLog对象的基数，则先判断对象头结构体中的基数缓存是否有效，如果有效，可直接返回。如果已经失效，则需要重新计算基数，并修改原有缓存，这也是PFCOUNT命令不被当做只读命令的原因。

结语

最后，给大家推荐一个帮助理解HyperLogLog原理的工具：http://content.research.neustar.biz/blog/hll.html，有兴趣的话可以去学习一下。

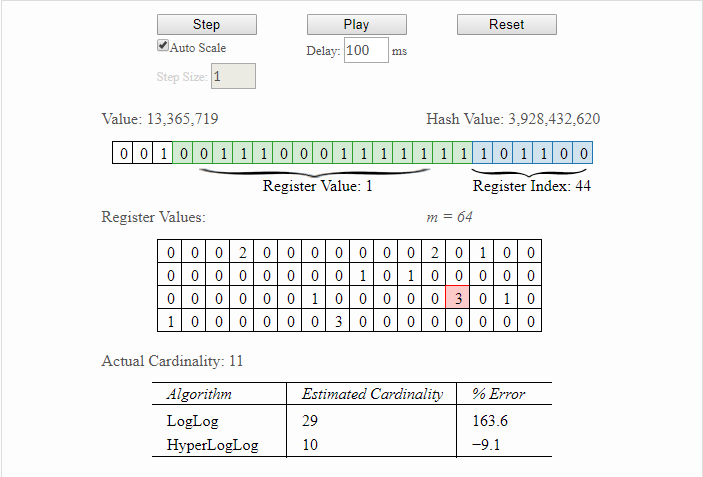
参考阅读

Redis new data structure: the HyperLogLog

探索HyperLogLog算法（含Java实现）

Redis 深度历险：核心原理与应用实践